This is the first post of a series I am writing about designing and running Cellular Automatons in an FPGA. I’ll end up with several variants, from one lighting up LEDs to another one drawing on a VGA monitor. But first, what is a Cellular Automaton?

I first heard of the concept of Cellular Automaton while watching an Electrical and Computer Engineering course lecture by Bruce Land (available on Youtube):

Some googling pointed me to this page on Wolfram with more details on the Cellular Automata.

Basically, in a Cellular Automaton, the value of the next evolution of a cell depends on the value of the cell itself, and the value of its adjacent cells.

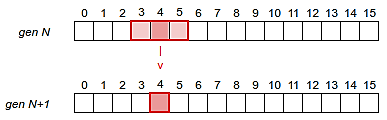
For example, let’s represent a one-dimension population of 16 cells (a line of cells) and let’s focus on cell 4:

The next generation of cell 4 will depend on the value of cell 4 and the two adjacent cells (cells 4 and 5):

Let’s now generalize to a row of N cells (or in other words, N-bits). To compute the next iteration of the first cell (0), we will simply take into account cells {N-1, 0, 1}. Likewise, to compute the next iteration of the last cell, N-1, we’ll take into account cells {N-2, N-1, 0} as shown below:

In the most simple form, each cell can have two values: 0 or 1, dead or alive. As we are looking at 3 cells, there are 2^3=8 posibilities of values for the triplet.

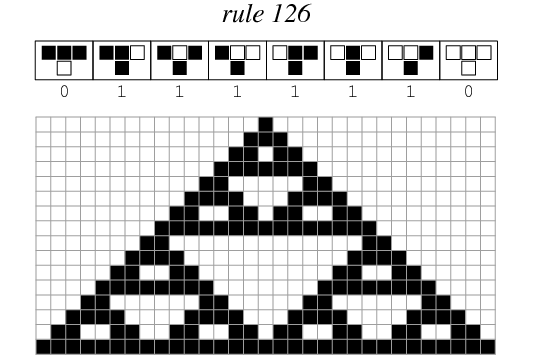
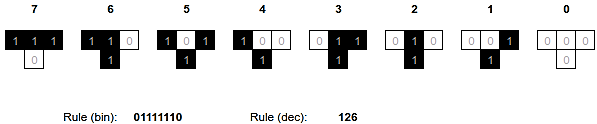
Let’s imagine an arbitrary rule for our Cellular Automaton: “the next generation of a cell will be 0 if the current generation of the cell is equal to the two adjacent cells”. In other words, if the 3 cells have the same value (0 or 1), the next generation of the cell will die (be 0). Otherwise, if at least one of the two neighbour cells is different, it will survive (be 1).

We can see that this rules makes the rule 126:

If we start with a black (1) cell at the center of the first line (generation 0), and we compute each succesive line with the rule above, we will obtain this drawing:

We have seen Rule 126. As we can see, a rule is actually a 8 bit value! So there are 256 different rules for a One Dimension Cellular Automaton.

Here are the results obtains for other rules:

In the next articles, I’ll describe a Cellular Automaton in Verilog and run it in an FPGA, output each generations on the LEDs or a VGA display.